유량 개요
2023.11.22 17:21- 작성자 관리자
- 조회 297
유량 기초 이론
유체를 정의한다면, 유체는 정지의 변형 압력을 견딜 수 없는 연속체 재질입니다.
회복할 수 있는 변형으로 된 변형 압력과 일치하는 탄성의 고체와는 달리, 유체는 회복할 수 없는 유량과 반응합니다.
유체와 유체의 환경을 정의하기 위해 필요한 변수는 다음과 같습니다.


예를 들어 유체가 가스와 액체를 포함할 경우, 전형적으로 유체가 압출될 수 없으나 가스는 압출 될 수 있습니다. 그러나 모든 엔지니어링 영역에서는 예외가 있습니다.
유량타입: 레이널드 지수
유체 유량은 얇은 층이거나 소용돌이 칩니다. 존재하는 유량의 종류를 결정하는 요인은 그 유체 안에서의 점성힘에 대한 관성의 힘의 비율입니다. 이는 치수로 잴 수 없는 레이놀드 지수에 의해 표현됩니다.
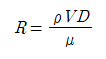
V와 D는 독특한 속도와 거리의 유체입니다. 파이프 안에 흐르는 유체에 대해 V는 평균 속도이며, D는 파이프 직경입니다.
대표적으로 유체 안의 점성의 stresses는 안정적이고 유량을 조직화 하려는 경향이 있습니다. 반면에 과도의 유체 관성은 제일의 조직화된 유량을 무질서한 소용돌이치는 상태로 왜곡시키는 경향이 있습니다.
유체 유량이 레이놀드 지수 2000까지는 얇은 층이며, 레이놀드 지수 4000 이상이면, 유량이 완전히 소용돌이칩니다. 레이놀드 지수가 2000과 4000 사이이면 유량은 얇은 층과 소용돌이치는 사이에서의 변화 과정에 있게 됩니다. 주어진 유량 범위 안에서 두가지 유량 타입의 생물(분포) 아구(亞區)를 찾기가 가능합니다.
방정식 적용하기
얇은 층의 유체 유량은 Navier-stokes 방정식에 의해 설명됩니다. 점착성이 없는 유량의 경우 Bernoulli 방정식이 유량을 설명하기 위해 사용됩니다. 유량이 제로일 때(예를 들어 유량이 변화하지 않는 경우), 유체는 유체 물리 정역학에 의해 적용됩니다.
| 다음글 | Navier stokes 방정식 | 2023-11-29 |
|---|


